Maths to get you through the coronavirus crisis
Katie Steckles
During this global pandemic, mathematicians and statisticians are providing a vital service in the form of mathematical modelling, in a worldwide effort to try to understand and fight the disease. But you may find mathematics is useful for surviving the pandemic in a more day-to-day fashion…
Distancing Yourself

One way to stop the virus spreading is through social distancing, and many governments are advocating that while people are out and about they try to maintain a two-metre distance from each other at all times. This means in theory each person is surrounded by a circular region of radius one metre, and if we can move around in such a way that these regions do not overlap, we’ll always be 2m away from everyone.
This kind of problem is called disc packing or circle packing, and there are many well-understood results in this area. For example, the most efficient way to arrange discs on an infinite plane, to fit the most discs in the space and leave the minimum area not covered by discs, is to pack them on the vertices of a hexagonal grid.
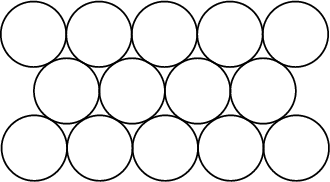
As seen in the diagram, this is a very efficient way to fill the space, and leaves only around 10% of the space unused. It was proven by Joseph Lagrange in 1773 that this is the most efficient arrangement for circles of equal size.
So if you’re standing in a large open space with other people, and want to maintain your 2m distance, the most efficient arrangement for you to stand in is at the corners of a hexagonal grid – each person should have six people around them, and if your arms are 1m long, you should just be able to touch the fingertips of each of the people around you (although obviously, don’t do that). This will allow you to fit the maximum number of people in the park without breaking the rules.
However, this result only works in the case of an infinite plane. If the region in which you’re standing has a boundary – like the walls of a room – the most efficient way to pack circles becomes a lot more complicated. Depending on the size of the room relative to your 1m radius circles, you may find that a regular lattice arrangement doesn’t give you the greatest efficiency, and depending on whether your room is square or circular, some suggestions are given on Wikipedia.

Densest packing of eleven congruent circles in a circle 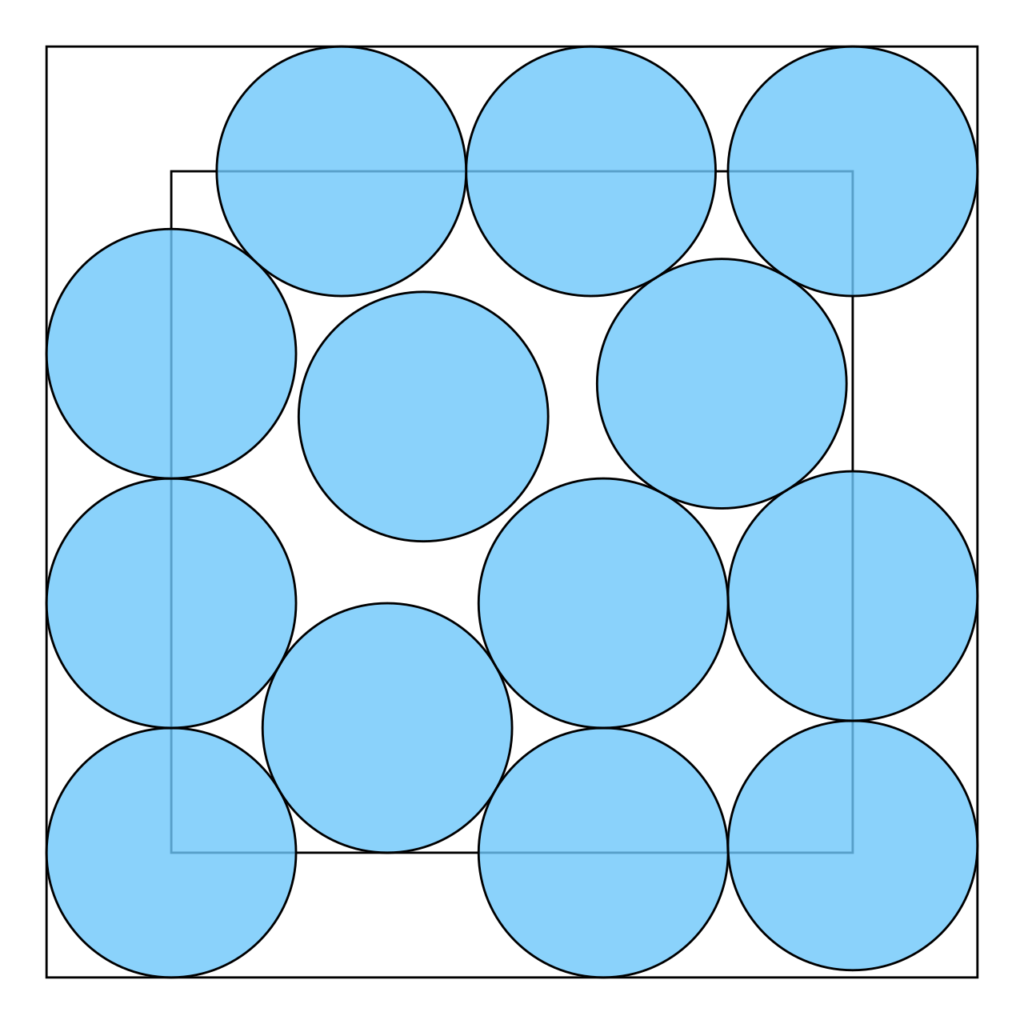
The densest packing of thirteen equal circles in a square
These examples show the most efficient way to pack unit circles into the smallest possible shape, so the size of the room will affect your best option. In general, finding an optimal packing arrangement is achieved by trial and error using computer algorithms – so make sure you take your laptop with you to the shops, and find a quiet spot outside to do your computations before attempting to enter the room.
Measuring your TP stash

One major concern for people in many areas at the moment is a shortage of toilet paper. Whether you believe this is caused by unscrupulous hoarders buying more than their fair share, or simply the increase in demand caused by everyone now spending all day at home instead of using the bathroom at work, applied to an already fragile supply chain – it makes no difference if you find yourself sitting next to an empty roll on the holder.
One way to combat this might be to keep a good eye on how much toilet paper you have left, and this paper “How Long is My Toilet Roll? – A Simple Exercise in Mathematical Modelling” discusses a way to answer this question, by asking: if I have a partly-used toilet roll, and know the radius of the roll of paper that’s left, can I work out how long the paper is (and crucially, how many sheets I have left)?
Modelling this is fairly simple – if you assign variables for the inner and outer radius (from the centre of the roll to the cardboard tube, and from the cardboard tube to the outside layer of paper), the thickness of the paper, and the number of layers, you can construct an equation to find the answer.
It’s slightly complicated to model, since the paper can be thought of as being in concentric circles around the roll (even though it’s actually a spiral, the numbers are very similar) but the radius, and hence the circumference of these circles, increases as you go more turns around the roll. One way to model this, discussed in the paper, is to find the average radius of these circles – halfway between the smallest and largest it could be, and assume they all have this radius. Doing so gives an equation which simplifies to:
Length of paper = (2π × R × n) + (π × n² × h)
Here, R is the radius of the inner cardboard tube, n is the number of layers of paper wrapped around the tube, and h is the thickness of one sheet. To find the number of layers, you can measure the outer radius and divide by the thickness of one sheet. Now, where are my precision calipers?
Timetabling your life
Many of you may now find that as well as your usual work, which you might be continuing with from home, you also have the responsibility of looking after, and potentially providing education for, one or more small humans. It may be that you’re finding it hard to work out how to schedule your day, plan lessons and also get your work done.
This kind of problem is faced by administrators in schools, universities and even businesses all the time – matching up lecturers or teachers with students taking different combinations of classes within their course, and finding the right sized rooms to put them all in, while making sure no lecturer or student is timetabled to be in two different places at the same time.
Timetabling falls into the category of a constraint satisfaction problem – correctly encoding and applying all of the necessary constraints to a set of teachers, students, rooms and classes and finding an algorithm to solve it, or at least come up with an arrangement that’s good enough. It’s such a big deal that there’s even an International Timetabling Competition, in which people compete to determine whose algorithms are best or most efficient.
If you’re struggling with this kind of logistics, mathematics can reassure you – the problem of timetabling is well understood and studied, and falls into a category of problems classed as ‘NP’. This is part of a categorisation of the complexity of problems which falls somewhere between maths and computer science – the computational complexity of a problem boils down to how many calculations a computer would need to do in order to solve it, or to check that the answer you’ve found is correct.
There are two main categories of problems: P and NP. P includes all problems that can be solved ‘efficiently’ – such as, ‘take two numbers and add them together’ – since this is one calculation for a computer to do. Efficiency, in this context, has a strict definition: if the number of calculations can be expressed in terms of the size of the input as a polynomial, that is, if the size of the input is x, the number of calculations is something like x² + 2x + 4 – rather than e.g. growing exponentially.
NP is the set of problems that, if you have a solution to them, you can efficiently check that the solution is correct. For example, the problem could be ‘given this set of numbers, can you split it into N smaller sets such that each one has the same sum?’. If you have a solution, checking it is as simple as finding the sum of each set and checking they’re the same. But finding a solution to an NP problem might be more complicated – the number of things to check, or calculations to do, could be too big.
Whether a problem is P or NP is an important distinction in the theory of complexity – one of the major unsolved problems in maths, and one of the Clay Institute’s Millennium Prize Problems, is the question of P vs NP – do polynomial time algorithms exist for solving NP problems – i.e. are P and NP the same thing? If anyone can answer this question (we think the answer is probably ‘no’, but we’re not sure) there’s a million dollar prize waiting for them.
The problem of timetabling can be shown to be NP – it’s equivalent to partitioning a set into triples, which is NP (many problems can be shown to be NP by finding an existing NP problem that they’re equivalent to when you boil them down to their simplest statement, like ‘match up students and lecturers with time slots and rooms’). So if you’re struggling to schedule everything – even if your class is small, and your room allocation options are limited – don’t worry: anyone would find this hard, and you’re doing a great job.
Der Beitrag Maths to get you through the coronavirus crisis erschien zuerst auf Heidelberg Laureate Forum.