An Elaborate Construction
Katie Steckles
When I was at school, we were given a required list of stationery to buy and bring in to school with us. This included a Maths Set – obviously, essential kit if you want to do maths – comprising a ruler, protractor, set square (sometimes two, if you got an expensive maths set) and a pair of compasses, for constructing circles. I treasured my Helix Oxford Set of Mathematical Instruments and proudly brought it to school with me every day.
I then went on to pursue a career in mathematics, and I can officially confirm that this equipment is in no way essential to anyone who wants to do maths. A drastically tiny amount of real maths actually involves constructing circles (and anyone who does tends to use geometry software anyway), and I don’t think any self-respecting mathematician would actually measure an angle with a protractor, since there’s usually some way to work out what it is exactly from other angles nearby.
So, while this equipment might be useful for someone working in illustration, or in drafting technical diagrams, it’s not really used for maths. However, a pair of compasses, or at least the concept of a pair of compasses, is part of a quite neat and enjoyable subset of geometry, called ruler-and-compass construction. And while it’s possible to use an actual ruler and pair of compasses for this, it’s much neater to use the abstract concept and – as is often most interesting – see where that takes you.
Rules and regulations
More correctly, the term is ‘straight-edge and compass construction’; the notional ruler in this universe doesn’t have markings on it in inches or centimetres, but is merely the concept of a straight line, which you can use to draw a line between two points. This gives us our first rule (no pun intended):
1. Given two existing points, we can construct a straight line that passes through those two points.
This is pretty much all we can get out of the ruler – it doesn’t really do anything else. The real interest comes when we bring in a tool for constructing circles – the pair of compasses.
Strictly, in the world of geometry, the compasses aren’t primarily a tool for drawing circles. What they really are is a tool for transferring distances. This means if I have two points a given distance apart, I can pick up that information and transfer it to somewhere else.
In particular, this means that if I keep one end of my compasses fixed on the page, the other end will trace out a circle shape, centred at the fixed point, with the radius as the distance between the two ends of the compasses. This is the definition of a circle – the set of all points that are the same distance away from a given centre.
So, now we can add another rule to our list:
2. Given two points, we can construct a circle which is centred at one of the points and passes through the other one.
Once we’ve started to construct things like lines and circles, we gain a few extra things we can do:
3. Given two non-parallel lines – or a line and a circle, or a pair of circles – which intersect, we can find and mark the point (or points) where they cross.
This set of basic tools allows us to construct things. Mathematics is often reduced to a game, in which you take a set of rules and play with them to see what you can do. In this case, mathematicians have thoroughly investigated the question ‘Given these tools, which things are possible to construct?’
Construction Toys
Obviously, to construct you need somewhere to start – so, let’s assume we start with two points, a given distance apart. If we call this distance ‘1 unit’, it’s possible to construct a line of length 2 units – since my compasses allow me to transfer a distance, I can simply copy the first distance again along the same line.
With a little more work, this also lets me construct a line of length 3, and in fact any whole number multiple of the original length. But it’s also possible to construct a line of any fractional length – for example, a line 2/7 units long. It’s even possible to construct a line whose length is the square root of a whole number – even if that length is irrational (can’t be expressed as a fraction), like the square root of 2.
As well as lengths, it’s possible to construct certain angles – for example, the construction of a right-angle (90 degrees) is a useful one to know.
Given a pair of points, you could join them with a line, then construct a second line which is always equidistant from both points. Given that every point on this second line needs to have that same property, all we need to construct it is to find two points with that property, then join them. So, we can set our compasses to an arbitrarily chosen length, and construct an arc centred at each of our two points – where they cross will be the same distance away from both the points.
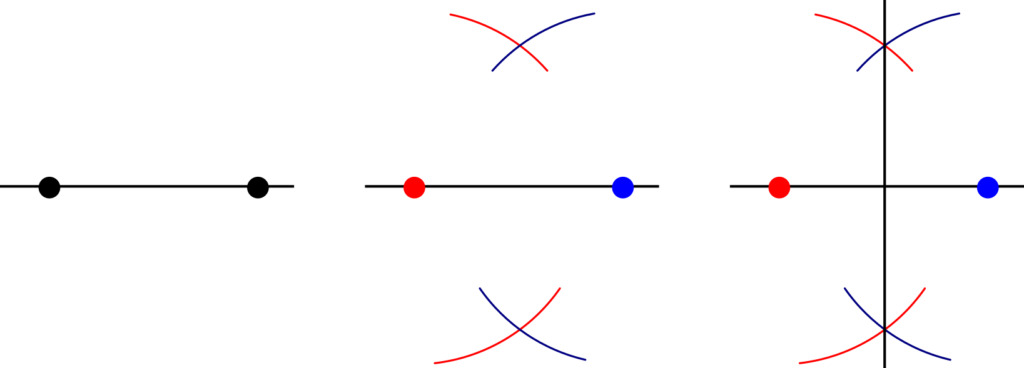
Do this twice, and you get a line which would bisect (cut in half) the line between your two points, and be exactly at right-angles to the first line you drew. This is called a perpendicular bisector, and can be built naturally as a consequence of our rules.
As well as a right-angle, you can construct a 60-degree angle (the angle in an equilateral triangle), and there’s even a slightly involved set of steps which will construct a 72-degree angle, which will allow you to construct a regular pentagon. The animation below shows the steps – each part of the construction is fairly simple, but once you’re in the middle of it you may start to wish you were allowed to use the protractor…

Circling the Problem
The really interesting question here though is, ‘Which things can’t I construct?’. You’d imagine that since we’ve got a few rudimentary geometrical tools, and maths is a logical subject, this might give us the ability to do anything we want. But that’s not the case, and some of the reasons why things can’t be done are linked to some very deep mathematics.
For instance, you may have heard the phrase ‘squaring the circle’ to mean solving a difficult problem. Well, it should really only be used when referring to a completely impossible problem! The question of ‘squaring the circle’ is actually asking, given a circle, is it possible to construct a square with precisely the same area. This is equivalent, in this universe, to being able to construct a length that’s π times longer than your original length. This has been proven impossible.
Another interesting impossibility is that of trisecting an angle. We saw how to bisect a line (find the middle point) and the same can be done with a given angle – finding a line that splits the angle exactly in half. However, even though it’s possible to split a line into equal thirds, it’s not possible to trisect an angle in this way. Again, a proof has been given of the impossibility of this, but it doesn’t stop people from occasionally making claims that they’ve done it (spoiler: they have not).
I mentioned that certain angles can be constructed – but not all angles can. The angles needed to construct an n-sided shape are given fractions of 360 degrees, and only some of these can be drawn using a ruler and compass. So even though, if you have the patience, you can construct a pentagon, there’s no method possible to construct a heptagon (a seven-sided shape). Of the numbers up to 20, it’s possible to construct shapes with 3, 4, 5, 6, 8, 10, 12, 15, 16, 17 or 20 sides – but none of the others.
The reasons for this link to a branch of mathematics called Galois Theory, which connects to the theory of groups and other algebraic structures; the formula for which numbers can be done (called ‘Constructible numbers’) involves Fermat primes, a particular type of prime number; and the question of which numbers are constructible boils down to the question of for which numbers n, cos(2π/n) has a repeating period which can be expressed in a series of quadratic equations with real roots, linking in trigonometry and algebraic geometry. This bridges several fields of maths and is a fascinating rabbit-hole of connections and results.
If you’re more interested in things that you *can* construct, I’d highly recommend this website, which features an interactive online tool which allows you to construct things in this universe, and even gives a series of challenges for you to try and complete using as few steps as possible. Or you can get out your Oxford Maths Set and try it by hand!
The post An Elaborate Construction originally appeared on the HLFF SciLogs blog.