Fun with False Proofs
Katie Steckles

This year’s HLF included a fascinating discussion between ACM AM Turing Award laureates Leslie Lamport and Whitfield Diffie, written up in full here by blog team member Andrei Mihai. As part of the conversation, when discussing how rigorous some proofs can be (and in some cases, not be), the topic of false proofs came up – with Lamport mentioning a particular example he’d seen in high school of a proof that all triangles are isosceles.
Shared a few years ago in a blog post from logician Joel David Hamkins, one such proof goes like this:
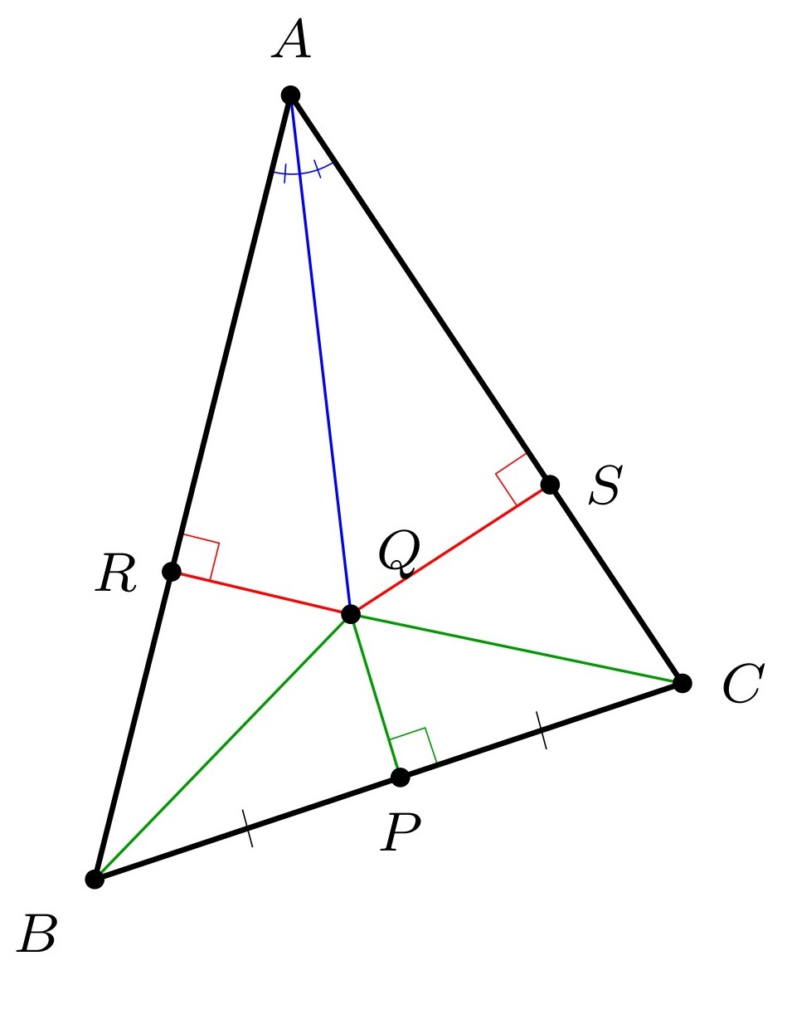
Consider an arbitrary triangle \(\triangle ABC\). Let \(Q\) be the intersection of the angle bisector (blue) at \(\angle A\) and the perpendicular bisector (green) of \(BC\) at midpoint \(P\).
Drop perpendiculars from \(Q\) to \(AB\) at \(R\) and to \(AC\) at \(S\). Because \(P\) is the midpoint of \(BC\) and \(PQ\) is perpendicular, we deduce \(BQ\cong CQ\) (they are congruent) by the Pythagorean theorem. Since \(AQ\) is the angle bisector of \(\angle A\), the triangles \(AQR\) and \(AQS\) are similar, and since they share a hypotenuse, they are congruent. It follows that \(AR\cong AS\) and also \(QR\cong QS\). Therefore the triangle \(\triangle BQR\) is congruent to the triangle \(\triangle CQS\) by the hypotenuse-leg congruence theorem. So \(RB \cong SC\). And therefore,
\[AB\cong AR+RB\cong AS+SC \cong AC\]
and so the triangle is isosceles.
You might be wondering where the error is here – I won’t give too much away, but it hinges on the position of the point Q – and this useful Geogebra applet, created by a commenter on Joel’s blog post following the description given in the proof, might be enlightening (so don’t open it unless you want a spoiler!)
This kind of ‘proof’ is often used as an amusing diversion by mathematicians – there’s humour in the contradiction of rigorous systems of mathematical proof being misused like this. They’re a popular diversion, as evidenced by the pages and pages of examples shared whenever people ask on maths websites. It’s also amusing to consider the obviously false conclusions you can reach – for example, here’s a proof that 1=2:
Let \(a=b\). Then
\(a^2 = ab\) (multiplying by \(a\) on both sides)
\(a^2 + a^2 = a^2 + ab\) (adding \(a^2\) to each side)
That is, \(2a^2 = a^2 + ab\)
Now subtract \(2ab\) from both sides:
\(2a^2 – 2ab = a^2 + ab\ – 2ab\)
That is, \(2a^2 -2ab = a^2 – ab\)
Then we can take out a factor of 2 on the left:
\(2(a^2 – ab) = a^2 – ab\)
Then dividing through by a common factor of \(a^2-ab\) on both sides, we have
\(2=1\).
The mistake in this one comes quite near the end – hopefully you can spot it. But as well as being an amusing diversion, these proofs also provide an insight into how mistakes can happen when writing proofs. It’s often a useful exercise for students to look through these ‘joke proofs’ and try to find the error – and when they spot it, it really hammers home the importance of checking everything you’re doing follows the basic rules of mathematics, otherwise you can find yourself proving something that’s clearly false.
This one, which I saw recently on Twitter, will really annoy pure mathematicians (but engineers might not mind too much!):
\[\begin{eqnarray*} x &=& \frac{(\pi+3)}{2}\\ 2x &=& \pi + 3\\ 2x(\pi-3) &=& (\pi+3)(\pi-3)\\ 2\pi x – 6x &=& \pi^2+9\\ 9-6x &=& \pi^2 -2\pi x\\ 9 – 6x +x^2 &=& \pi^2 -2\pi x + x^2\\ (3-x)^2 &=& (\pi – x)^2\\ 3-x &=& \pi – x\\ \pi &=& 3 \end{eqnarray*}\]
(This one involves another of the classic easy-to-miss errors, but I won’t tell you where it is!)
Of course, the risk with sharing these might be that people are intimidated by the possibility of making a mistake in a mathematical proof. Leslie Lamport said “[When I saw the isosceles triangle proof] I realised that you could not believe a single proof that you wrote in your high school plane geometry class – none of them are rigorous”. While this is more a comment on the level of rigour employed at that level of maths education than a lack of belief in his own abilities, it’s possible that the realisation of how easy it is to make these errors might cause some mathematicians to doubt themselves.
The important thing to remember is that mistakes, while very possible and reasonably common – Lamport himself estimates that roughly a third of all published refereed mathematical papers contain an incorrect theorem – are an important part of the process of learning how to do mathematics (although I guess it would be better if they didn’t actually make it out into the literature!)
By studying these incorrect proofs, we can learn what the common pitfalls are. The Wikipedia page on mathematical fallacies lists common numerical and geometrical errors – including some evidenced in the examples given here – and I’ve run sessions with my students before which include a chance to find and correct errors in other people’s work, which have helped them develop the confidence to look for and fix errors in their own.
I’ll leave you with one final fun fallacious proof, and it’s a classic (and this time, it’s not even proving a false conclusion):
\[ \require{cancel} \frac{16}{64} = \frac{1\cancel{6}}{\cancel{6}4} = \frac{1}{4}\]
QED.
The post Fun with False Proofs originally appeared on the HLFF SciLogs blog.