Maths on a Plate
Katie Steckles
If you’ve ever been to the Heidelberg Laureate Forum, you’ll know that one of the best parts of the experience (apart from, obviously, the wonderful lectures and panel discussions and the chance to meet and network with all the great people there) is the food. Every meal includes a delicious buffet or three-course extravaganza, in beautiful surroundings and joined by the aforementioned great company.
But the HLF is about maths and computer science, not food, you might be thinking. Well, as I’ve previously noted in blog posts here, it’s often possible to find mathematical ideas during the meals – and not just from the conversation. At this year’s HLF, I found my breakfast one day was served to me on a plate with a mathematical shape to it…
My plate, it has three corners
The vast majority of tableware (including the saucers and side plate also visible in this photo) stick to a sensible circular shape. It’s symmetrical, and hasn’t got any corners, and is easy to manufacture and stack in a dishwasher. Roundness, it seems, is a quality cherished in plates.
But my breakfast plate is triangular: it has three notable ‘corners’, with curved sides in between. You might imagine that such a shape couldn’t possibly be considered to be as round as a circle. But mathematically, this shape is more round than you might think!
The shape is called a Reuleaux triangle. It’s named after 19th-century German engineer Franz Reuleaux, and can be constructed starting from an equilateral triangle. Drawing a circle centred at one corner of the triangle, whose radius is equal to the length of one side of the triangle, will create a curved arc which passes through the other two corners of the triangle. The Reuleaux triangle is formed from three arcs constructed in this way, one from each of the corners of the underlying equilateral triangle.
ALT: Video showing the construction of a Reuleaux triangle, as described above, one circle at a time
This construction produces a pleasing shape, and it has some interesting properties. It is known to mathematicians as a shape of constant width, which means that if you measure the widest part of the shape in any direction, by bringing two parallel lines together either side of it until they hit the shape, you’ll get the same measurement. All the points along each curved side of the shape are the same distance from the opposite corner – by virtue of the way it was constructed.
This means that if you roll a Reuleaux triangle along the ground, its highest point will always be at the same height. It also means that this shape is – by some measure – round. A circle is another example of a shape of constant width, although it has the additional property that the midpoints of the lines describing the diameter of the shape all lie in the same place. On the Reuleaux triangle, the ‘centre’ of the shape moves depending on which way up it is.
Reuleaux whyangle?
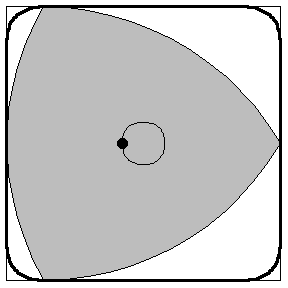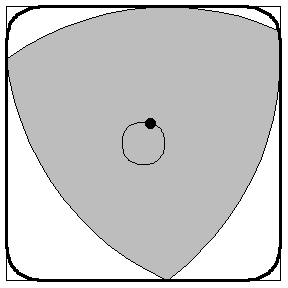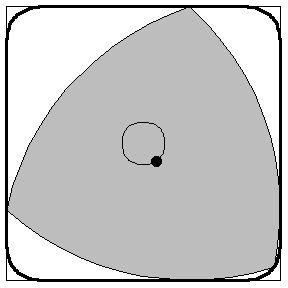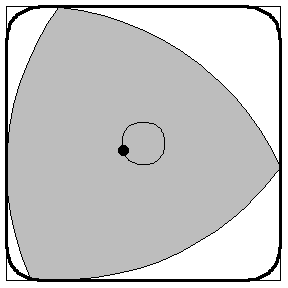
This shape has some interesting technical applications. For example, a drill bit with a Reuleaux triangle-shaped head mounted on can drill square holes; Reuleaux himself used the shape in machines for translating one type of motion into another, and they have applications in film projection; they appear in the configurations of soap bubbles and in the centre of a three-way Venn diagram, and they’re used as the shape of guitar picks, windows and some company logos. They’ve also been used as a shape for the nuts on fire hydrants to prevent people opening them without a special tool.
This shape is also part of a family of more general shapes of constant width, which can be based on any regular polygon with an odd number of sides. They’re constructed in much the same way, using arcs of circles centred at the opposite corner. All these shapes have the same property that their width is the same in every direction, and this construction can be extended to irregular polygons too, and also to even-numbered sided shapes if the arcs are constructed in a slightly different way.
Seven-sided shapes of constant width are used as the shape of 50p and 20p coins in the UK, and one country has even historically had a Reuleaux triangle-shaped coin (as you may have guessed, it was Bermuda). These shapes are useful as coins, since it allows vending machines to measure the width of the coin and be sure which coin it is (rather than risking a shape of variable width, which might get measured a different way up!)
It is also possible, given the shapes’ constant width, to use them as wheels – although since the centre isn’t fixed in place, you can’t use the standard axle-based mechanism. If you’re prepared to have the frame of the bike resting on top of the wheels, and can construct a frame to hold it in place and power the wheels, there’s no reason you couldn’t make a bicycle with wheels of constant width – and if you’d like to see one, this video of a triangular-wheeled bike from Burning Man in 2012 has got you covered.
You might argue that I’m just someone who has seen too much interesting mathematics, and that everywhere I go I’ll read maths into what I’m seeing – including the plate I get my breakfast on. But I like to think that the world is full of interesting things that can be described using mathematics, and it’s a pleasure to be able to notice things like this and share them with the people around me. As long as we finish breakfast in time to get to the first HLF lecture of the day…!
The post Maths on a Plate originally appeared on the HLFF SciLogs blog.
