Die Entdeckung der holomorphen Funktionen

Christoph Pöppe

Werden die Gegenstände der Mathematik erfunden oder entdeckt? Das ist eine Frage, über die man trefflich streiten kann, wie nicht nur die professionellen Philosophen, sondern auch die zahlreichen Kommentatoren meines letzten Beitrags eindrucksvoll bewiesen haben.

Wer Mathematik studiert, bekommt vom ersten Tag an mit großer Deutlichkeit die Ansage vermittelt, dass – zum Beispiel – die natürlichen Zahlen erfunden werden. Mehr noch: Was man in seinem bisherigen Leben über die natürlichen Zahlen entdeckt hat – und das ist in der Regel nicht wenig –, könne man getrost vergessen. Hier werde die Mathematik von Grund auf neu aufgebaut, und über die natürlichen Zahlen sei nur das von Bedeutung, was die Peano-Axiome dazu sagen. Und überhaupt habe Mathematik mit der erfahrbaren Realität nichts zu tun; vielmehr seien ihre Gegenstände freie Schöpfungen des Geistes und sonst gar nichts.

Damit wäre die Sache eigentlich klar – wenn nicht die Praxis dieser fundamentalistischen Haltung so krass widersprechen würde. In der täglichen Arbeit treten mir die Funktionen, Gleichungen, Differenzialoperatoren und so weiter, die ich mir wohlgemerkt selbst definiert habe, als Objekte außerhalb von mir gegenüber. Sie sind eigenwillig, manchmal überaus widerspenstig und zeigen unangenehme Eigenschaften, die ich ihnen niemals hätte andefinieren wollen. Und das geht nicht nur mir so. Welcher Mensch, der bei Verstand ist, hätte sich freiwillig mit so schrecklichen Dingen wie unsäglichen Zahlen und unmessbaren Mengen eingelassen? Nein, die kamen mit in dem Paket, das die Mathematiker selbst bestellt und dessen Inhalt sie vor allem selbst angefertigt hatten. Die Unsäglichen und Unmessbaren waren sozusagen eine unvermeidliche Zugabe. Und die wollte erst entdeckt werden!

In diesem Fall war die Entdeckung sogar schmerzhaft für die Entdecker. Georg Cantor, der Schöpfer der modernen Mengenlehre, sah, dass es verschiedene Grade der Unendlichkeit gibt, und konnte es zuerst nicht glauben – so ein berühmt gewordener Ausspruch von ihm. Und bis seine Kollegen es glauben konnten, gab es erbitterten Streit.

Selbst wenn man eine längst etablierte Entdeckung nur nachvollzieht, kann es sich wie ein echtes Entdeckungserlebnis anfühlen. So ging es mir, als wir im 4. Semester Funktionentheorie lernten. Die Bezeichnung dieses Teilgebiets ist übrigens hoffnungslos irreführend, aber wohl nicht mehr auszurotten. Es geht nicht um irgendwelche Funktionen, sondern um eine sehr spezielle Sorte. Man nennt sie komplex differenzierbar. Sie sind auf den komplexen Zahlen definiert und haben komplexe Werte. Darüber hinaus müssen sie nicht nur differenzierbar sein; ihre Ableitungen müssen auch noch ein relativ einfaches Paar von Gleichungen erfüllen: die Cauchy-Riemann-Differenzialgleichungen.

Na gut; wie das in der Mathematik so üblich ist, bekommt man zunächst eine Definition wie „komplex differenzierbare Funktion“ kommentarlos hingeknallt. Womit es nun ausgerechnet diese spezielle Sorte Funktionen verdient hat, dass man sich so ausgiebig mit ihr beschäftigt: Das kommt später.
Und in diesem Fall kommt sehr viel. Komplex differenzierbare Funktionen sind nicht nur einmal differenzierbar, sondern unendlich oft. Und wenn man die unendlichen vielen Ableitungen in einem einzigen Punkt hat, dann kann man die Funktion in einer Umgebung dieses Punktes „in eine Potenzreihe entwickeln“. Es handelt sich im Prinzip um dieselbe Reihe, die auch unter reellen Funktionen als Taylorreihe bekannt ist: eine unendliche Summe aus relativ einfachen Termen.

Wenn der Punkt, um den herum die Funktion entwickelt wird, der Nullpunkt ist, dann ist jeder Term eine Konstante mal eine Potenz von z. Damit komplexe Funktionen auf den ersten Blick erkennbar sind, pflegt man ihre unabhängige Variable z zu nennen statt x bei den reellen Funktionen. Man kann sie allerdings um jeden Punkt entwickeln, der nicht gerade am Rand ihres Definitionsbereichs liegt. Nennen wir ihn z₀; dann ist jeder Term der Potenzreihe eine Konstante mal eine Potenz von (z–z₀).
Vielleicht konvergiert die Potenzreihe nur in einer kleinen Umgebung von z₀ (die unendliche Summe muss ja einen endlichen Wert haben, und das wird zunehmend schwieriger, je größer z–z₀ wird). Aber durch fortgesetztes Umrechnen der Entwicklungen kann man sich von einem Punkt zum nächsten hangeln, und wenn es keine Hindernisse gibt, erzählen einem die Werte der Funktion und ihrer Ableitungen in einem einzigen Punkt alles über die Funktion in der ganzen komplexen Ebene. Und wenn die Funktion zwischendurch unendlich wird, muss dies nicht unbedingt ein Hindernis sein. Erst wenn sie das auf besonders üble Weise tut (eine „wesentliche Singularität“), wird es kompliziert.

Andererseits sind komplex differenzierbare Funktionen „schrankenlos“, ganz im Gegensatz zu ihren reellen Kolleginnen. Eine Funktion wie sin x oder 1/(1+x²) wird nie größer als 1 und nie kleiner als –1 – für reelle Werte von x. Im Komplexen schlagen sie beide über die Stränge. Und das ist so etwas wie eine Standardeigenschaft komplex differenzierbarer Funktionen. Die einzigen in der ganzen komplexen Ebene beschränkten Funktionen dieser Klasse sind die Konstanten, also die Langweiler, die überall denselben Wert annehmen.

Alle diese schönen Dinge sind definitiv nicht erfunden, sondern entdeckt worden. Wir wissen das, weil die Funktionenklasse mehrere verschiedene Namen hat. Man nennt sie außer „komplex differenzierbar“ auch „komplex-analytisch“ oder „holomorph“. Warum? Weil die einen Mathematiker sich mit den Funktionen beschäftigten, welche die Cauchy-Riemann-Gleichungen erfüllen, die anderen mit denen, die in eine Potenzreihe entwickelbar sind – und erst hinterher bemerkten, dass beide Seiten über dieselbe Sache reden! Natürlich war da der Jubel groß.

Ein naheliegender Einwand könnte den Jubel empfindlich dämpfen. Wer äußerst restriktive Bedingungen stellt, braucht sich nicht zu wundern, wenn die wenigen Objekte, die diese Bedingungen erfüllen, eine Fülle von angenehmen Eigenschaften haben.

Ein Beispiel aus einer ganz anderen Ecke der Mathematik: Wie man zum Teil schon in der Schule lernt, gibt es besondere Punkte im Dreieck, solche, in denen sich jeweils drei Geraden schneiden, von denen man das nicht unbedingt erwartet hätte: Schnittpunkt der Mittelsenkrechten, der Winkelhalbierenden, der Höhen, der Seitenhalbierenden … Angeblich steht die Zählung dieser Punkte bei über 47000. Na gut. Für ein gleichseitiges Dreieck fallen alle diese Punkte in einen zusammen. Das ist nett, aber nicht wirklich ein Anlass zum Jubel. Stellst du maximale Forderungen, kriegst du maximale Ergebnisse – für das eine Objekt, das diese Forderungen erfüllt.

Sind also die komplex-analytischen Funktionen ein kleiner Kreis von erlesenen Gestalten, die man nur unter exotischen Umständen überhaupt antrifft? Ganz im Gegenteil – und das ist der eigentliche Grund zum Jubel. Alle Feld-, Wald- und Wiesenfunktionen, die man so aus der Schule kennt, gehören dazu: die gemeinen Potenzfunktionen, Sinus und Cosinus, die Exponentialfunktion und der Logarithmus, und dann alles, was man aus ihnen durch Addieren, Subtrahieren, Multiplizieren, Dividieren und Ineinandereinsetzen zurechtbasteln kann. Vorausgesetzt, man schreibt sie wie gewohnt als Funktion einer einzigen Variablen (die man, wie gesagt, z zu nennen pflegt).

Nicht vergessen: Eine komplexe Zahl sind ja eigentlich zwei reelle, Real- und Imaginärteil. So gesehen haben unsere Funktionen zwei unabhängige und zwei abhängige Variable, sind also eigentlich Paare von Funktionen zweier Variablen namens x und y. Und irgendwelche Paare solcher Funktionen sind noch lange nicht komplex-analytisch. Vor allem aber lassen sich komplexe Funktionen nicht so bequem darstellen wie die reellen. Papier und Computerbildschirm haben eben nur zwei Dimensionen und sind deswegen mit einer reellen Funktion – eine Achse für x, die andere für f(x) – bereits ausgelastet. Eine Funktion von zwei reellen Variablen wäre noch darzustellen als so ein Gebirge über der (x, y)-Ebene, und mit etwas Mühe gibt eine perspektivische Zeichnung davon zumindest einen Eindruck von ihrem Verhalten. Eine richtig komplexe Funktion wären dann zwei Gebirge über derselben Ebene, und einerlei, ob man die nebeneinander zeichnet oder einander durchdringend: So wirklich erhellend ist das nicht, weswegen man solche Diagramme kaum zu sehen bekommt.

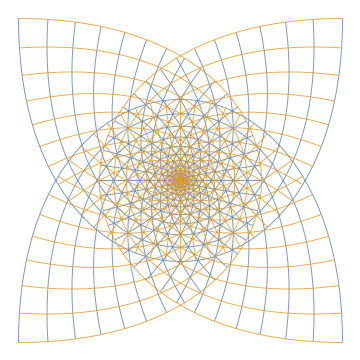
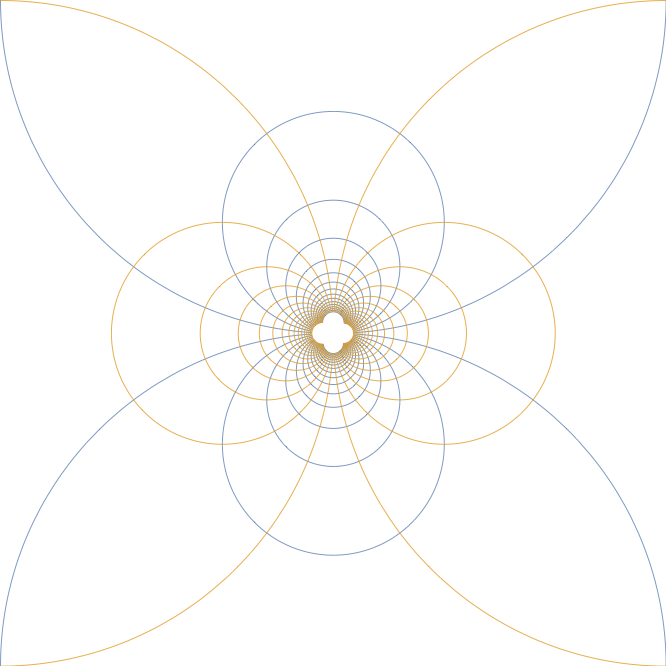
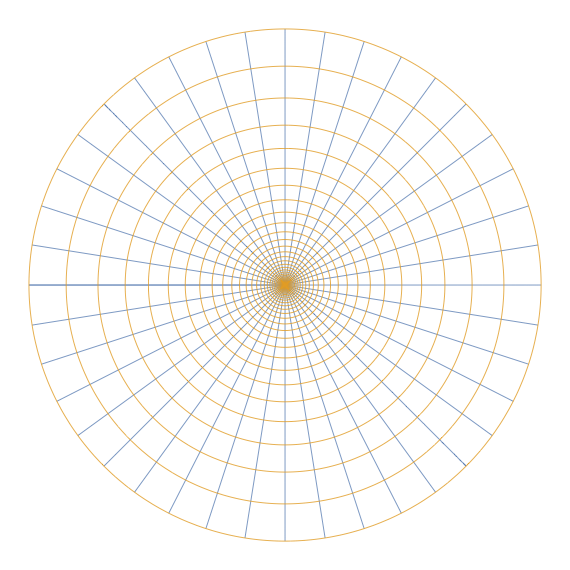
Was man stattdessen machen kann, ist eine Punktmenge in der Ebene nehmen und aufzeichnen, auf welche Menge sie durch eine komplexe Funktion abgebildet wird. Auf die Idee bin ich gekommen, nachdem wir gerade Funktionentheorie gelernt hatten und ich Zugriff auf ein damals sehr avanciertes computergesteuertes Zeichengerät hatte (die graphische Benutzeroberfläche lag noch in ferner Zukunft). Was ich damals mit ziemlich viel Mühe programmiert hatte, war mit heute aktueller Hard- und Software sehr einfach nachzuvollziehen. Als Punktmenge nahm ich ein Stück Quadratgitter („Rechenkästchen“).

Das Urbild: f(z) = z

Und wenn man f(z)=z² darauf anwendet? Dann hat das Kissen nur noch zwei Zipfel statt vier.

f(z)=z²

Schon richtig, z und –z werden auf denselben Punkt abgebildet; das gilt insbesondere für einander gegenüberliegende Kissenzipfel. Und ehemals gerade Linien findet sich als die wohlbekannten quadratischen Parabeln wieder.

f(z)=z³ rührt das ganze große Quadrat so intensiv um, dass sein Rand sich dreimal statt vorher einmal um den Nullpunkt windet.

f(z)=z³

Mit f(z) = √z wird es komplizierter. Eigentlich gibt es zu jeder komplexen Zahl zwei Quadratwurzeln, die sich nur durchs Vorzeichen unterscheiden, wie bei den positiven reellen Zahlen halt. Der Eindeutigkeit zuliebe muss man sich auf eines der Vorzeichen festlegen, und üblicherweise wählen die Computerprogramme von den beiden Möglichkeiten die mit dem positiven Realteil. Aus dem Rechenkästchenquadrat wird damit eines, das sich nur ein halbes Mal um den Nullpunkt windet, und zwar auf der rechten Seite. Dafür muss es gewissermaßen entlang der negativen reellen Achse geschlitzt werden, was sich in dem Bild durch den dicken vertikalen Strich bemerkbar macht. Damit das halbe Quadrat nicht so einsam aussieht, habe ich das Bild unter f(z) = –√z mit dazugetan.

f(z)=±√z

Die Funktion f(z)=1/z kehrt das Innere zuäußerst und umgekehrt.

f(z)=1/z

Die Exponentialfunktion macht aus den horizontalen Linien Strahlen in alle Richtungen und biegt die vertikalen zu perfekten Kreisen.

f(z)=exp z

Und der Sinusfunktion sieht man an, dass sie von der Exponentialfunktion abstammt. Immerhin zeugt der waagerechte Strich in der Mitte davon, dass die reelle Sinusfunktion (reelle) Werte zwischen –1 und 1 annimmt.

f(z)=sin z

Auf allen Bildern sieht man, dass rechte Winkel rechte Winkel bleiben – was eine weitere unter den erfreulichen Eigenschaften holomorpher Funktionen ist. Irgendwann haben die Mathematiker entdeckt, dass diese Funktionen sogar allgemein „winkeltreu“ („konform“) sind – bis auf spezielle Punkte.

Na gut, so habe ich persönlich die holomorphen Funktionen und etliche ihrer Eigenschaften entdeckt. Nicht dass das eine besondere Leistung gewesen wäre, aber es war eben eine Entdeckung, an erfundenen Gegenständen. Worauf ich mit diesem Beitrag hinauswollte.

Was die bildliche Darstellung holomorpher Funktionen angeht: Das können inzwischen andere Leute viel besser, allen voran Elias Wegert, Professor für Mathematik an der TU Bergakademie Freiberg (Sachsen). Ich habe im August 2018 einen Artikel über seine Werke geschrieben. Zu dumm nur, dass die Website der TU Ende Januar einem Cyberangriff zum Opfer gefallen ist. Damit ist bis heute (27. 3. 2023) die überaus reichhaltige Sammlung seiner Bilder unter www.mathe-kalender.de nicht erreichbar. Ich werde Sie auf dem Laufenden halten.

The post Die Entdeckung der holomorphen Funktionen originally appeared on the HLFF SciLogs blog.