A Question of Curvature
Katie Steckles
People are often interested in mathematical ‘life hacks’ – ways they can use mathematics to make their life easier. For me a much more interesting conversation results when there is a hack people already know about and use all the time, which they didn’t realise was actually quite inherently mathematical.
This occurred to me recently when I was thinking about Gaussian curvature. This is a geometrical property of objects and surfaces which describes how the surface curves in three-dimensional space. Gaussian curvature is the answer to a very specific definition: if an object curves in one direction, what does it do in the other direction?
Are You Being Curved?
To find the Gaussian curvature at a point on a given shape, you need to measure two perpendicular axes of curvature; for those of you holding a sharpie pen and/or who would like a simpler way of phrasing that, you need to draw a cross on the shape, made from two lines which intersect at right angles.
Once you’ve picked a point and drawn a cross, you need to compare how those two lines curve in 3D. Imagine your object is a shape like a sphere – a football, a bowling ball or an orange – and that you’ve drawn your cross on the very top of it. The two lines will both be curving downwards as they move away from the centre of the cross.
How much are they curving by? Well, we measure the curvature of a circle as 1/r, where r is the radius of the circle. So each line is curving at a rate of 1/r in the same direction. The Gaussian curvature is calculated as the product of these principal curvatures: for two identical curves, 1/r × 1/r = 1/r², which for any sensible value of r will be a small but definitely positive number.
This is because a sphere is an example of a shape which has positive Gaussian curvature, and hopefully with a little thought you can convince yourself that it will remain true whichever point on the sphere you choose: if it curves away from you in one line, the perpendicular line curves away from you too. This means the sphere has positive Gaussian curvature everywhere.
If instead we wanted a shape with zero Gaussian curvature, we could picture something flat – a piece of paper, a section of floor (in most sensible places), or a pizza. If we measure the curvature in two directions at a chosen point, it will be zero, and the product of zero with itself is still zero. But you didn’t need me to tell you that something which does not curve has no curvature.
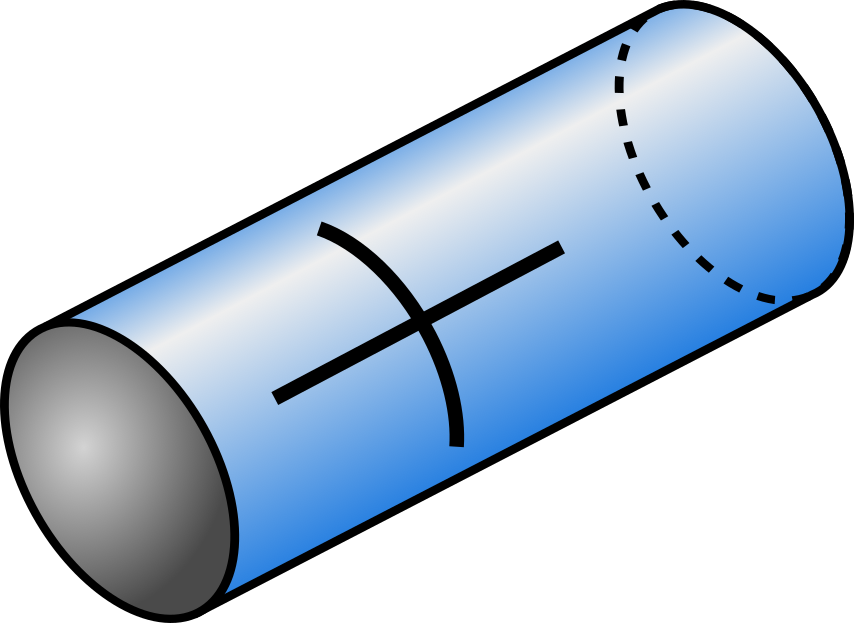
Imagine instead a shape like a cylinder: a rolled-up tube of paper, a pencil or a fancy cylindrical pillow. If we pick a point on the flat end of the cylinder, that will also have zero curvature, just like on our flat objects. But if we pick a point on the curved side, and draw a cross there, something interesting happens.
Taking The Tube
To find the principal curvatures, we need to look for a maximum and a minimum: this forces the orientation of our cross to have one line running horizontally parallel to the cylinder’s length, and the other one wrapping around the cylinder’s circular face (On the sphere, the curvature is the same in every direction, so the orientation of the cross is unimportant).
Since we have a curve in one direction, the curvature is 1/r (where r is the radius of the cylinder). But in the other direction, it will be zero – and 1/r times zero is just zero. So even though a cylinder has a curved face, when considering Gaussian curvature, it isn’t curved at all. And this is where things start to get interesting – because Gaussian curvature is an intrinsic property of an object and cannot be changed.
So if I start with a piece of paper, and want to curve it into a cylinder, I can do that pretty easily: a cylinder has the same curvature as a flat object, so it will do this with no problems. However, if I tried to curve it further – into a donut shape or a sphere, things would start to get messy – the paper would need to be crumpled, or cut, or torn and stuck together, in order to create the shape.
As anyone who has tried to peel an orange will tell you, you don’t get a whole piece of flat peel; similarly, anyone who has attempted to map the globe will quickly have found that in order to draw it all on a flat page, you need to stretch and squash parts of the surface, or leave gaps along the edge (á la the magnificent Goode homolosine projection). An object with positive curvature can’t map onto an object with zero curvature, and vice versa.
So if you have an object with zero curvature, it will always have zero curvature: if you bend it in one direction, it will remain steadfastly straight in the perpendicular direction. And if this sounds like a familiar idea, that will be because it is something you have very likely used regularly without even thinking about it as a ‘life hack’, namely when eating a pizza.
I deliberately included pizza on my list of zero-curvature objects, because a pizza, and indeed a single slice of pizza, is a flat object with the zero curvature property. And if you pick up a piece of pizza by its crust, you might find it starts to unhelpfully droop, threatening to discharge all of its delicious toppings onto the floor. In this situation, the solution is simple: introduce curvature in a perpendicular direction.
Again, translating that into a more sensible instruction: bend the crust of the pizza upwards at the sides. This will make the pizza curve in that direction, meaning that according to the rules of geometry, it will not be able to curve in the direction at right-angles to that: along the length of the slice.
Of course, this depends slightly on the sogginess of your pizza dough: a soft, stretchy base will rashly ignore the universe’s rules of geometry and probably stretch and curve in whichever directions it wants. But assuming a reasonably structurally intact pizza base, this ‘hack’ has been used by millions of people around the world to prevent their slice from drooping. But how many of them, I wonder, credit Carl Friedrich Gauss with its success?
The post A Question of Curvature originally appeared on the HLFF SciLogs blog.