Pioneering Graph Theory – László Lovász
Sophie Maclean
László Lovász is an accomplished man: He won the Abel Prize in 2021 alongside Avi Wigderson, another laureate who attended the 10th Heidelberg Laureate Forum (HLF) this year; he was President of the International Mathematical Union from 2007 to 2010; and he is also a favourite of attendees at the HLF.
Lovász gave his lecture, titled “From Puzzles to a New Paradigm”, on the Thursday of the HLF. I had not met Lovász before, but from the affectionate way every other journalist and HLF regular said his name, I knew that I was in for a treat.
Lovász and Wigderson were awarded the Abel Prize for their work in discrete mathematics. This is a broad area of mathematics including topics such as theoretical computer science, number theory, and combinatorics. But it was the applications of his research in graph theory that Lovász spoke about at the Forum, and it was also this that first introduced me to Lovász.
Graph Theory 101
Graph theory, unsurprisingly, studies graphs. But possibly not the type of graphs you are thinking of. The graphs I am referring to here are a collection of dots (usually called vertices or nodes) with edges between them.
Formally, we would say that a graph \(G = (V,E)\) where \(V\) is the set of vertices, and \(E\) is the set of edges. Each edge \(e\in E\) is a pair of vertices \( (v_1,v_2)\) with \(v_1,v_2 \in V\). Unless specified, the edge is an unordered pair – \( (v_1,v_2)\) is considered to be the same as \( (v_2,v_1)\). If the edge is an ordered pair, we call the graph a directed graph (or digraph for short) and as the name implies, this can be intuitively thought of as each edge having a direction. If you want to learn more about directed graphs, you can read Katie Steckles’ excellent blog post from the HLF last year. Here though, I am going to focus on undirected graphs.
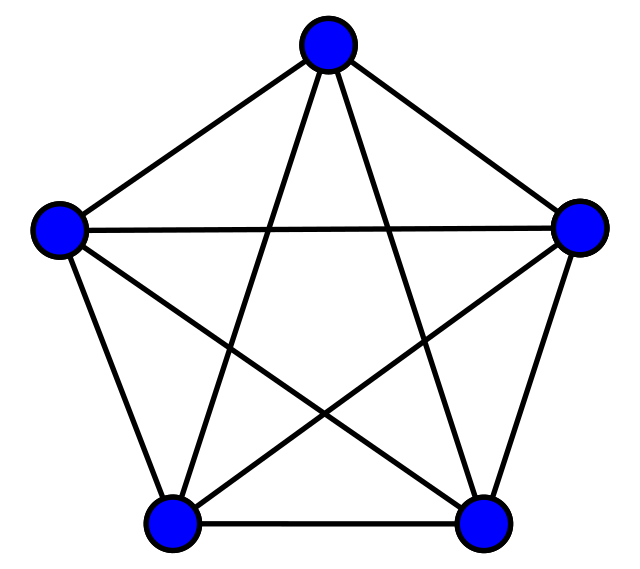
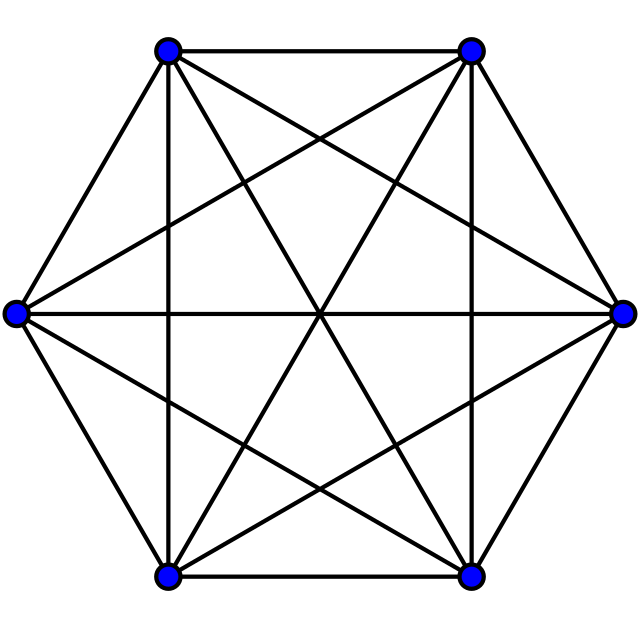
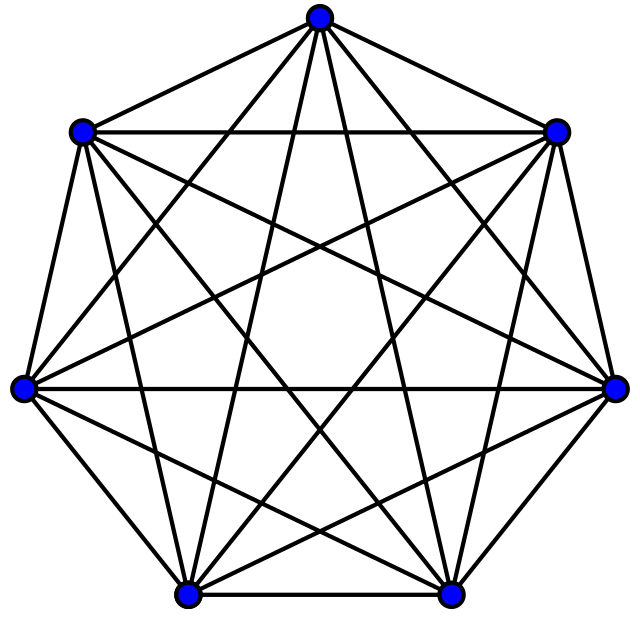
There is a special name used for a graph with \(n\) vertices and all possible edges drawn in: the complete graph (of order \(n\)). This is denoted by \(K_n\). The number of edges is \(n(n-1)/2\). This is because each of the \(n\) vertices is joined to all of the \(n-1\) others, however we divide by two because we want to view the edge from, say, \(v_1\) to \(v_2\) as being the same as the edge from \(v_2\) to \(v_1\).
Ramsey Theory
Many questions in graph theory boil down to determining the relationship between the properties of a graph and the patterns that can be found within it. For example, you might ask how many edges does a graph with \(n\) vertices need, to guarantee that a triangle exists? I’ll let you have a go at working out the answer to this, but if you would like a hint, start with small \(n\) and get drawing!
Ramsey theory is a subfield of graph theory focussed on precisely questions like this. Ramsey theory starts with the complete graph \(K_n\) and colours each edge one of two colours (say, red or blue). It then asks what the smallest value of \(n\) is that is required for there to be either a red \(K_s\) or a blue \(K_t\) for some positive integers \(s,t\). This is denoted by \(r(s,t)\).
For example, if \(s=2\) and \(t=3\), it asks for the smallest \(n\) such that there must be a red line or a blue triangle. A quick think will tell us that, for these criteria not to be satisfied, all edges must be blue. In a complete graph with all blue edges, if there are \(3\) or more vertices then there must be a blue triangle. Note that \(2\) vertices are not enough, as we can colour the edges of \(K_2\) in a way that has no red line or blue triangle. So \(r(2,3) = 3\).
Local Lemma
I first came across László Lovász during my masters in mathematics course, when I took a module titled “probabilistic methods in combinatorics”. In 1975, Lovász came up with a powerful theorem called the “local lemma”. The theorem is (loosely) as follows:
Let \(A_1,\dots A_n\) be events that could occur. Suppose that \(p \in [0,1)\) and \(d\) is an integer such that: for all \(i\), \(\mathbb{P}(A_i)\leq p\); \(A_i\) is mutually independent of a collection of all but at most \(d\) other events \(A_j\); and \(ep(d+1)\leq 1\) where \(e\) is Euler’s number. We write \(A_i^C\) to denote the event that \(A_i\) doesn’t happen. Then
\[\mathbb{P}\bigg(\bigcap_{i\in \{1,2,\dots,n\}}A_i^C\bigg)>0. \]
This is a very powerful theorem, and it has some applications in Ramsey Theory too!
Suppose we have \(K_n\) and we colour the edges red or blue randomly and independently (with probability \(1/2\) for each colour). For a set \(S\) of \(k\) vertices, we shall let \(A_S\) denote the event that the edges in \(S\) are either all blue or all red. There are two colours, and \({\begin{pmatrix} k \\ 2\end{pmatrix}}\) edges, so \(\mathbb{P}(A_S) = 2 \cdot \frac{1}{2}^{\begin{pmatrix} k \\ 2\end{pmatrix}} = 2^{1 – \begin{pmatrix} k \\ 2\end{pmatrix}}\). Note that \(A_S\) is mutually independent of all \(A_T\) for \(T\) a set of \(k\) vertices not sharing any edges with \(S\) (i.e. with \(|S\cap T | \leq 1\)).
Note that all sets of \(k\) vertices that do share an edge with \(S\) can be found by choosing an edge in \(S\) (which there are \({\begin{pmatrix} k \\ 2\end{pmatrix}}\) ways of doing) and then choosing the remaining \(k-2\) vertices from all \(n\) vertices of the graph. Subtracting \(1\) to ensure we do not count \(S\) itself, there are at most \({\begin{pmatrix} k \\ 2\end{pmatrix}}{\begin{pmatrix} n \\ k-2\end{pmatrix}} – 1\) sets of \(k\) vertices that do share an edge with \(S\), though this is likely to be an overestimate. Now we can apply the local lemma!
Take \(p = 2^{1 – \begin{pmatrix} k \\ 2\end{pmatrix}}\) and \(d = {\begin{pmatrix} k \\ 2\end{pmatrix}}{\begin{pmatrix} n \\ k-2\end{pmatrix}} -1\), do a bit of algebra, and we see that, so long as \(e\cdot 2^{1 – \begin{pmatrix} k \\ 2\end{pmatrix}}\cdot{\begin{pmatrix} k \\ 2\end{pmatrix}}{\begin{pmatrix} n \\ k-2\end{pmatrix}} < 1\), then
\[\mathbb{P}\bigg(\bigcap_{\text{all } S}A_S^C\bigg)>0. \]
In other words, the probability that the edges in \(S\) are not either all blue or all red for all \(S\) is positive. So when this criteria is met there exists a graph for which there is no red \(K_k\) or blue \(K_k\). Hence if \(e\cdot 2^{1 – \begin{pmatrix} k \\ 2\end{pmatrix}}\cdot{\begin{pmatrix} k \\ 2\end{pmatrix}}{\begin{pmatrix} n \\ k-2\end{pmatrix}} < 1\), then \(r(k,k) >n\).
Erdos Renyi Random Graphs
In his lecture at the HLF, Lovász introduced the audience to random graphs. There are, as you’d expect, different types of random graphs, depending on whether the randomness is applied to the vertices, edges or even the direction of the edges if we consider a digraph. Even within the set of random graphs for which the randomness is applied to the edges, there are many different ways of deciding whether or not a given edge is included, for example one must decide whether or not all the edges appear with probabilities independent of each other.
The Erdos–Renyi (sp) random graph \(\mathcal{G}(n,p)\) is a graph on \(n\) vertices where each two vertices are joined by an edge independently with probability \(p\). The expected number of edges of a random graph is therefore \(pn(n-1)/2\), i.e. the total number of edges on a complete graph, multiplied by \(p\).
Random graph methods can be applied to problems similar to those in Ramsey theory. This time though, we simply want to know whether we can find \(K_m\) within our random graph, for some positive integer \(m\). How we go about this, though not necessarily too mathematically complicated, can get a bit fiddly. For those interested in the technicalities, it uses some theorems known as Markov’s inequality and Chebyshev’s inequalities, but I won’t get bogged down in the details. It is the results that are interesting. For example, we can show that if \(n^2p^3 → 0\) as \(n → ∞\) then, with probability tending to \(1\), \(\mathcal{G}(n,p)\) has no copy of \(K_4\).
Why do we care? Well once we know about properties of random graphs, we can predict the properties of unknown graphs. This is a very useful thing to be able to do.
A New Paradigm
During his lecture, László Lovász spoke about the history of graph theory and how it is going to be even more important in the future. Network theory is an offshoot of graph theory and the two are incredibly closely related as networks are just (sometimes very large) graphs.
When you think of networks, you may well think of social networks or computer networks. But there are many, many more examples: There are ecological networks; the universe is a network; your brain is a network. Given how all-encompassing the study of networks is, it is easy to see how significant it is. With further developments in astronomy, computing, and medicine, it is also easy to see how the applications of network theory can only grow.
His research into network theory took Lovász on a journey through mathematics to computer science, optimization, and even physics. Who knows where else it will take him!
The post Pioneering Graph Theory – László Lovász originally appeared on the HLFF SciLogs blog.